Mathematics is the language of all sciences, without it, no science would have evolved to its present state. Just as the alphabet is fundamental in learning to read and write, so does mathematics form the basis of all physical and applied fields.
It is a rigorous science in the sense that problem solving is achieved with strict rules of logic and that is why those who solve a problem correctly must find the same result. This rationalization, far from subjectivism and interpretation, was one of the reasons I loved mathematics.
In order for a person to be able to evolve in this area, it is necessary to understand the rules as memorization has minimal benefit. That is why it is crucial for the teacher to be able to develop ways of learning that, on one hand, stimulate interest, and on the other hand, help to understand the course material for the student. I have been working on this part for the last 10 years or so, having developed methods based on multisensory learning.
Multisensory learning is one of the most effective ways of teaching [1, 2, 3]. More specifically, I create material such that the student perceives and processes information with as many senses as possible.
Below are some examples of how I teach.
Example 1: The meaning of Limit | Concerns: Students & Graduate Students
Definition of limit of a function through animated graphics. When the distance (h) of 2 consecutive points is relatively large, the definition of the limit (yellow box) deviates from the actual value f'(1) = 5. However, as the distance decreases, the limit tends to become equal to the actual value. If h becomes so small that it is considered 0, then the red line is the tangent of the function to x = 1. This is why the limit
As a consequence of the above, when the red line (tangent) becomes parallel to the x-axis then the function f(x) does not change around this point so f(x) = f(x0) and the limit gets to 0.

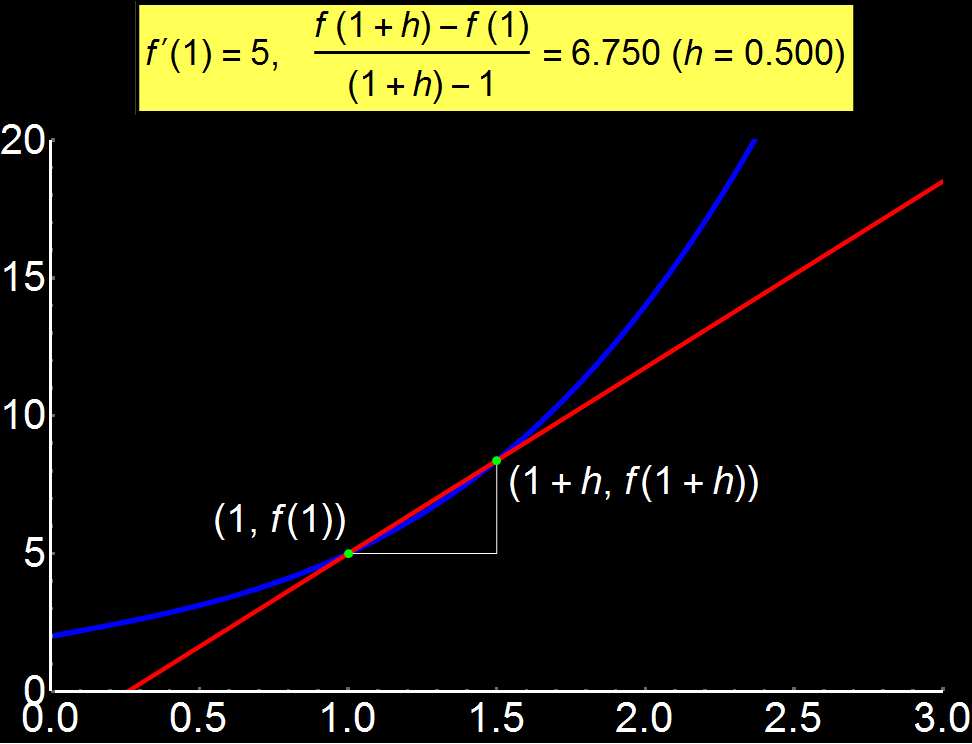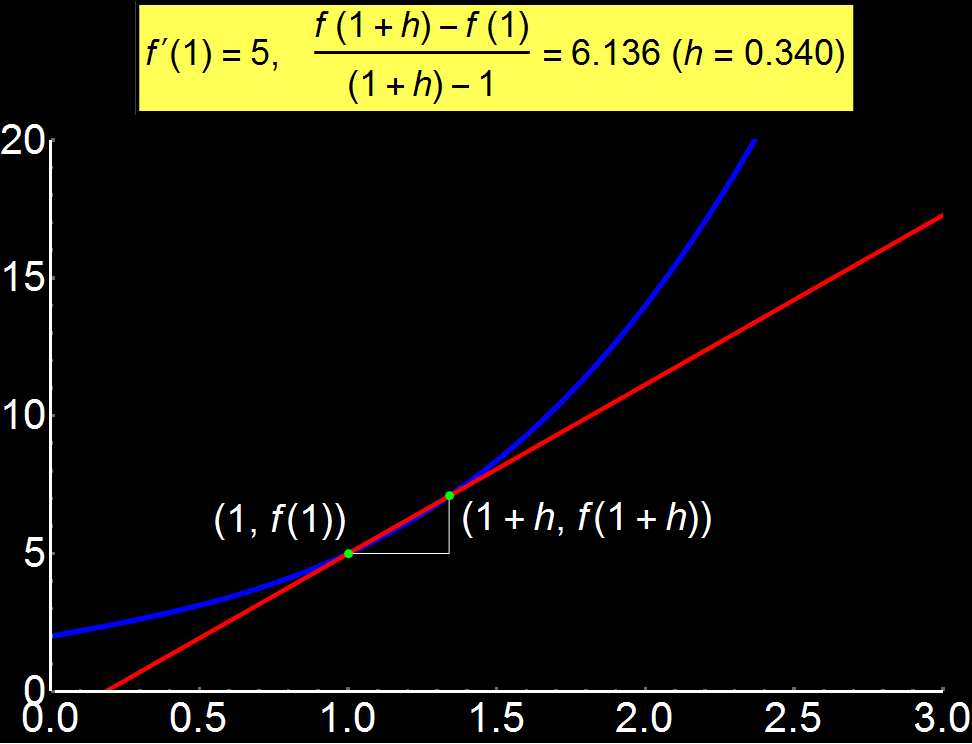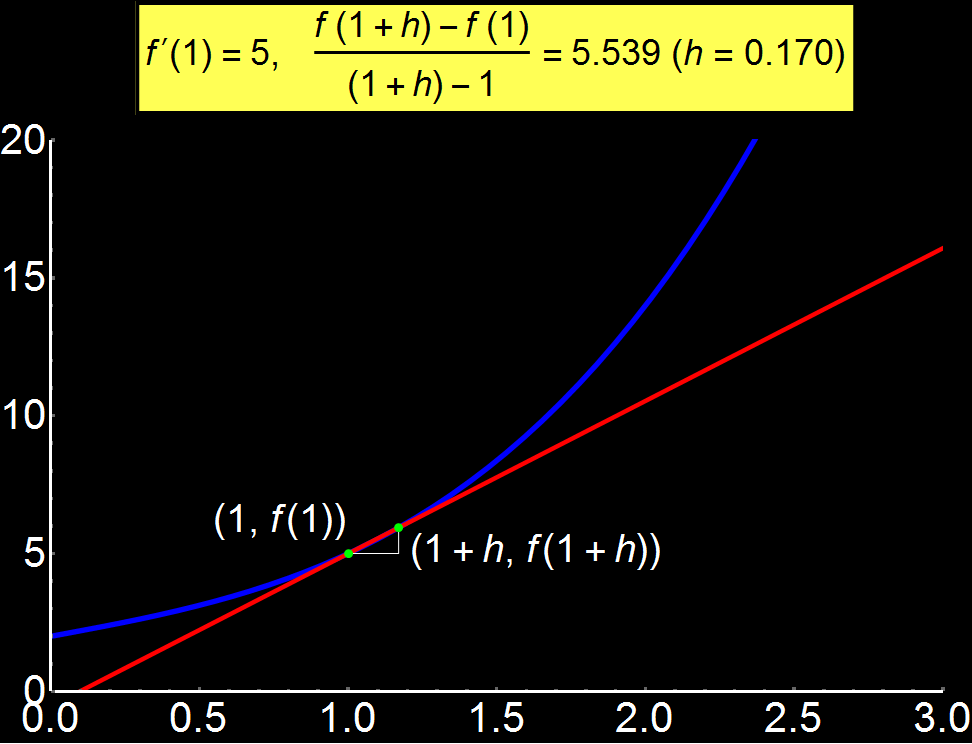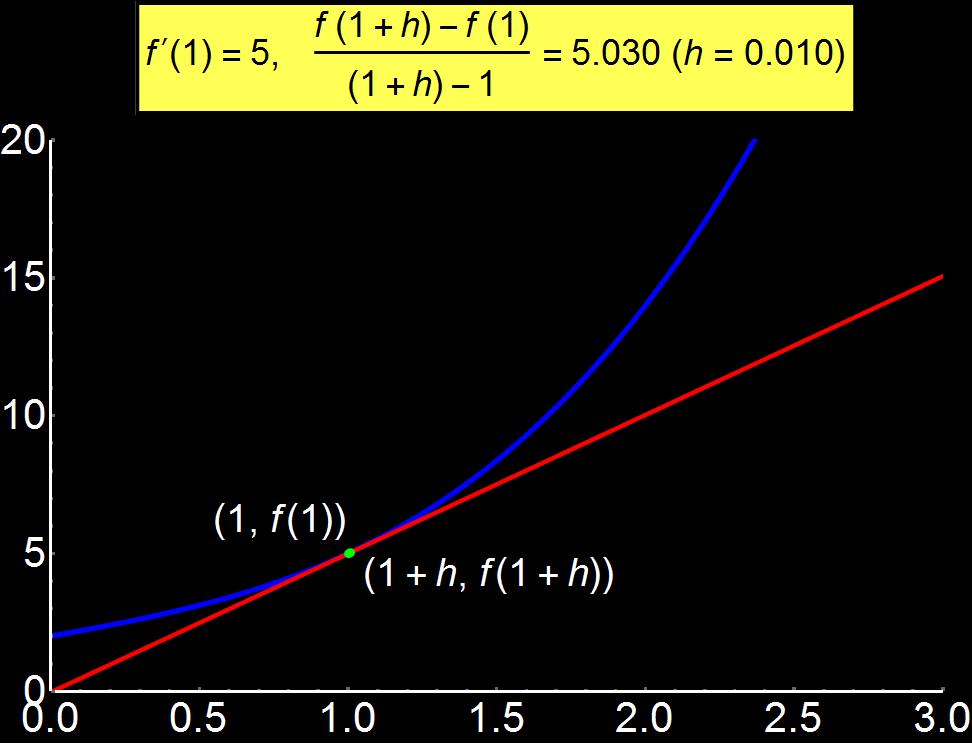
Conversely, in the case where the red line is parallel to the y-axis then the variable x does not change around this point so x = x0 vanishing the denominator and so the limit is not defined.
Example 2: The meaning of Integral | Concerns: Students & Graduate Students
Definition of integral is one of the most difficult concepts for a student. In the adjacent graph I show that, by increasing the discretization (number of gray rectangles), we can gradually approach the exact solution of the integral of a function (see yellow box). Therefore, the more gray rectangles we have, the better the convergence of the approximate value with the analytical integral. In the limiting case where the number of rectangles tends to infinity we have:

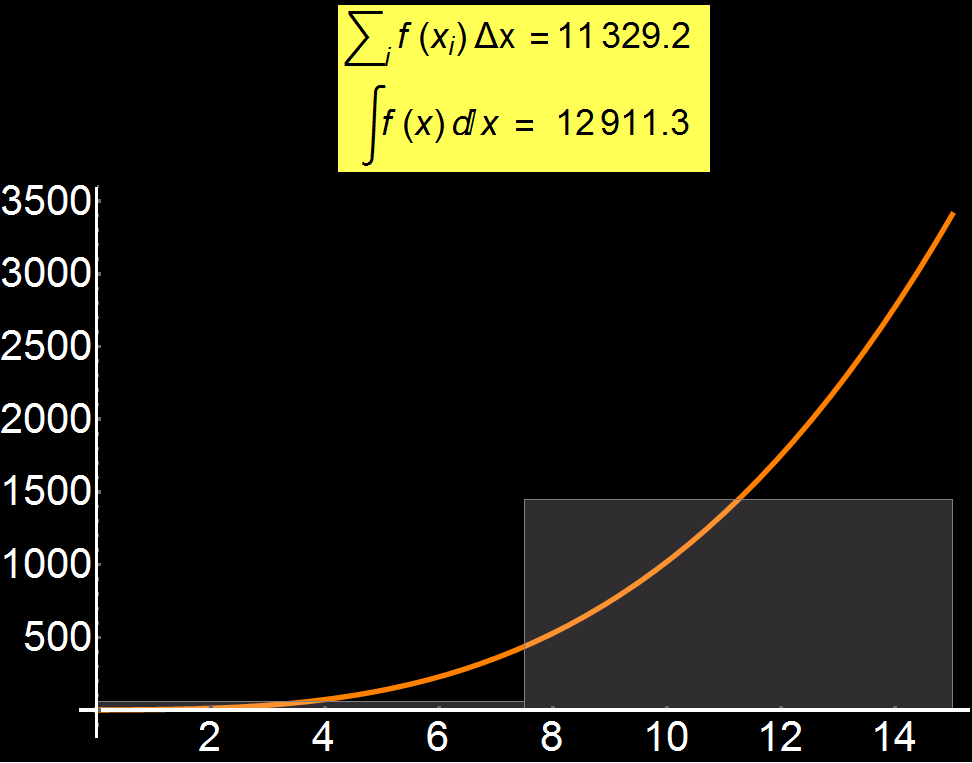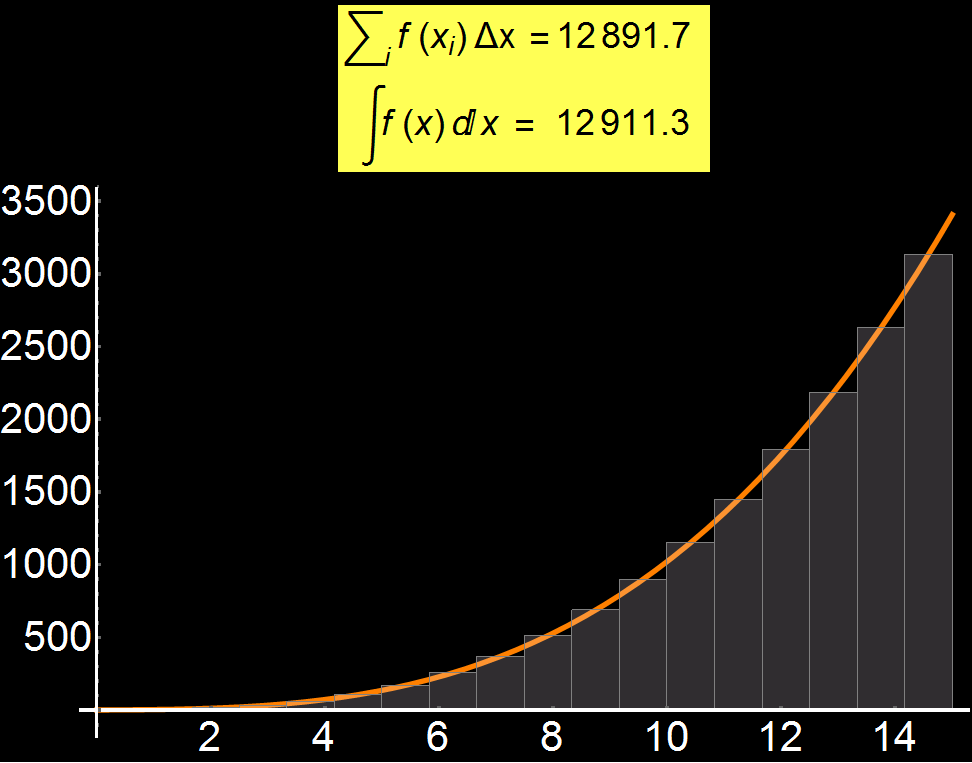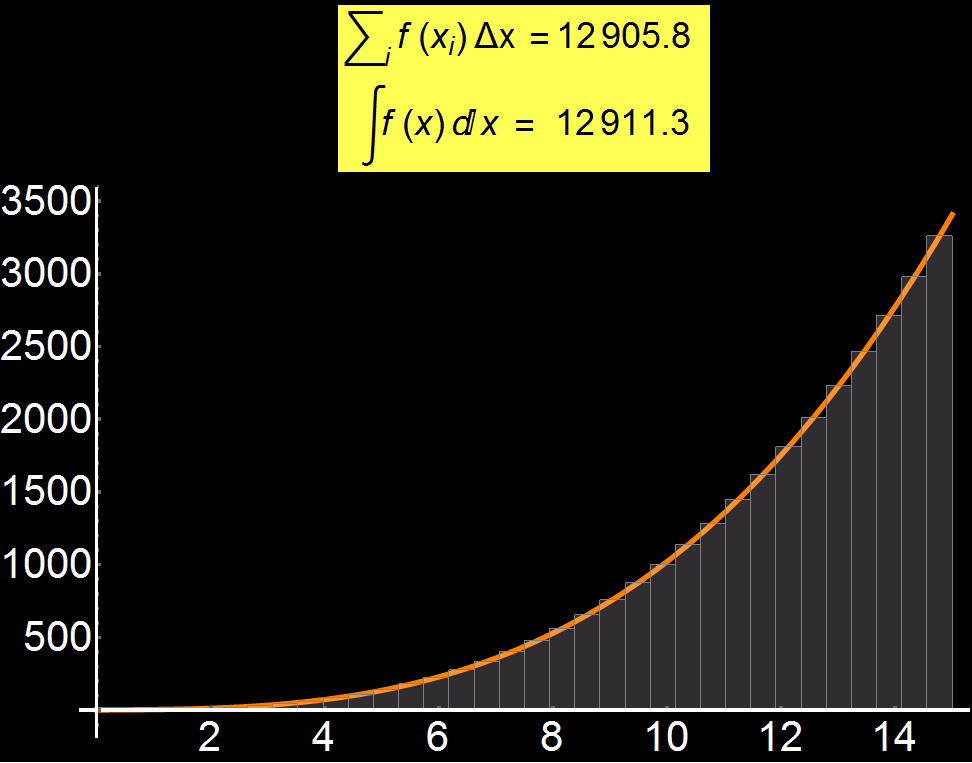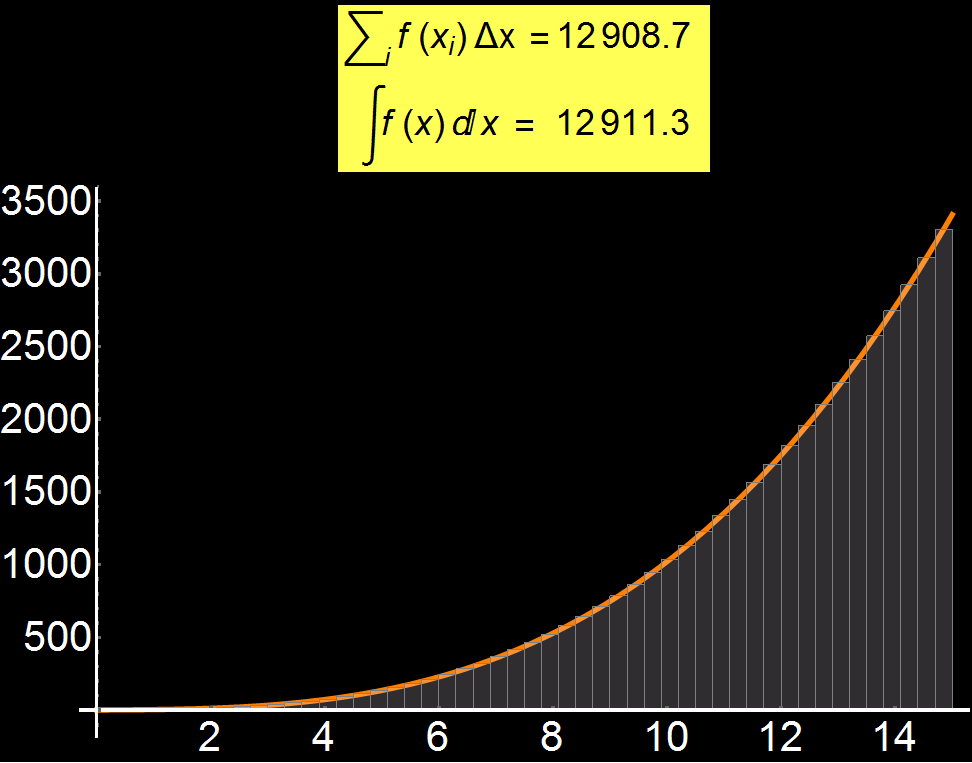
In many practical problems, the integral is impossible to be calculated analytically and so numerical approaches like the one I show here are used.
Example 3: Tangent Equation | Concerns: Students & Graduate Students
Tangent equation to a function f(x) shows us its slope at each point {x0, f(x0)}. In other words, it tells us how 'steep' the function is at each point. It is given by the expression:
In the adjacent graph I show how the tangent (red line) changes as it 'scans' a function f(x) (blue curve). We observe that around the values +3 and -3 the blue curve changes abruptly, as a consequence, the numerical value of the slope of the tangent eq. takes large values (f'(x0) ~ 400). In contrast, around 0 where the blue curve changes slightly, the slope exhibits small values (f'(x0) ~ 1).
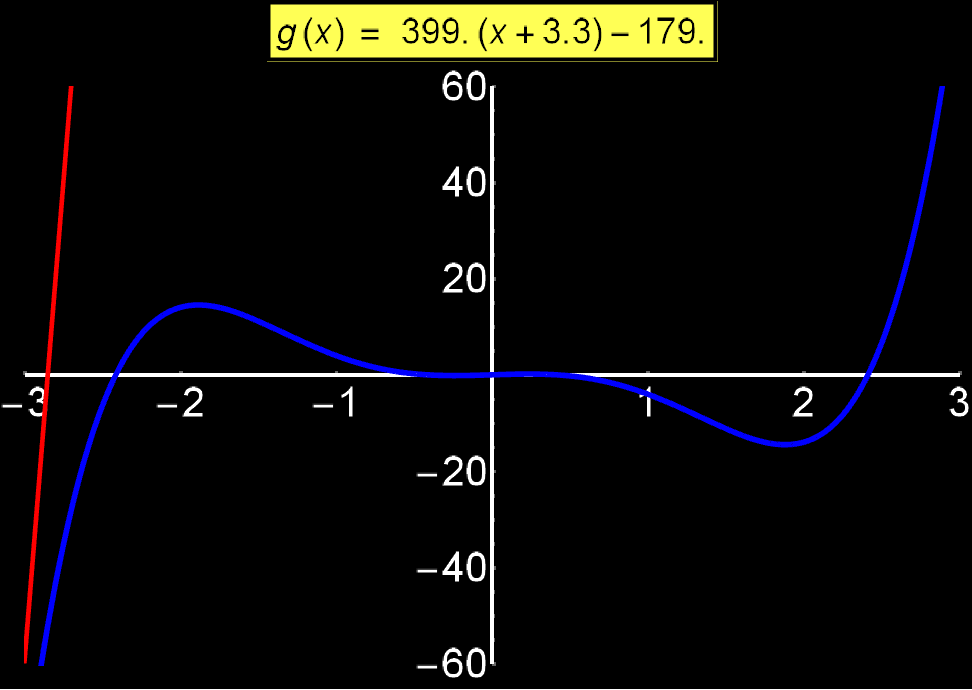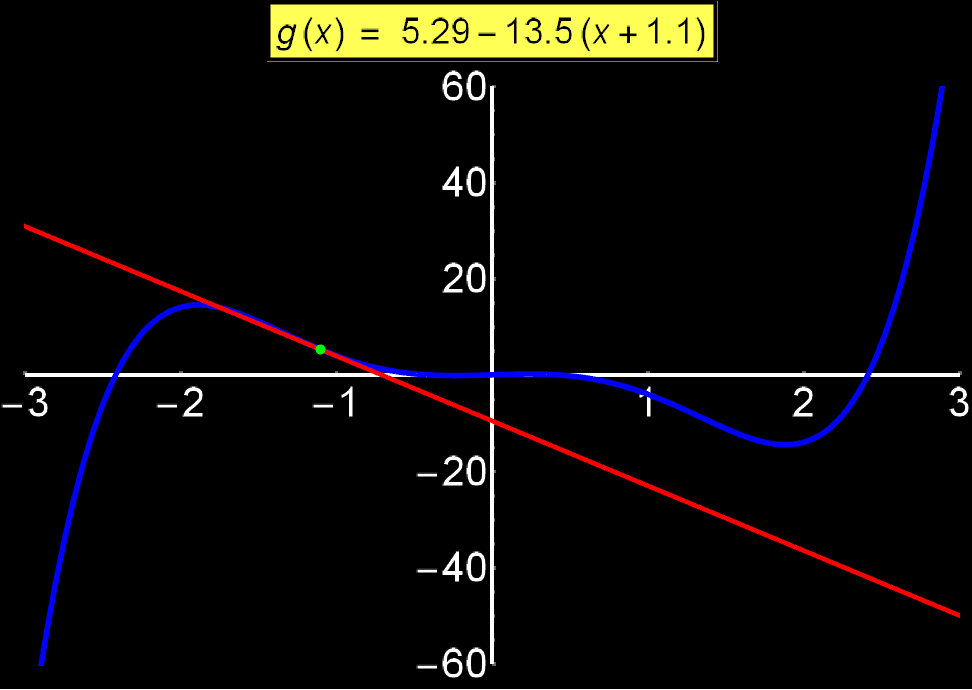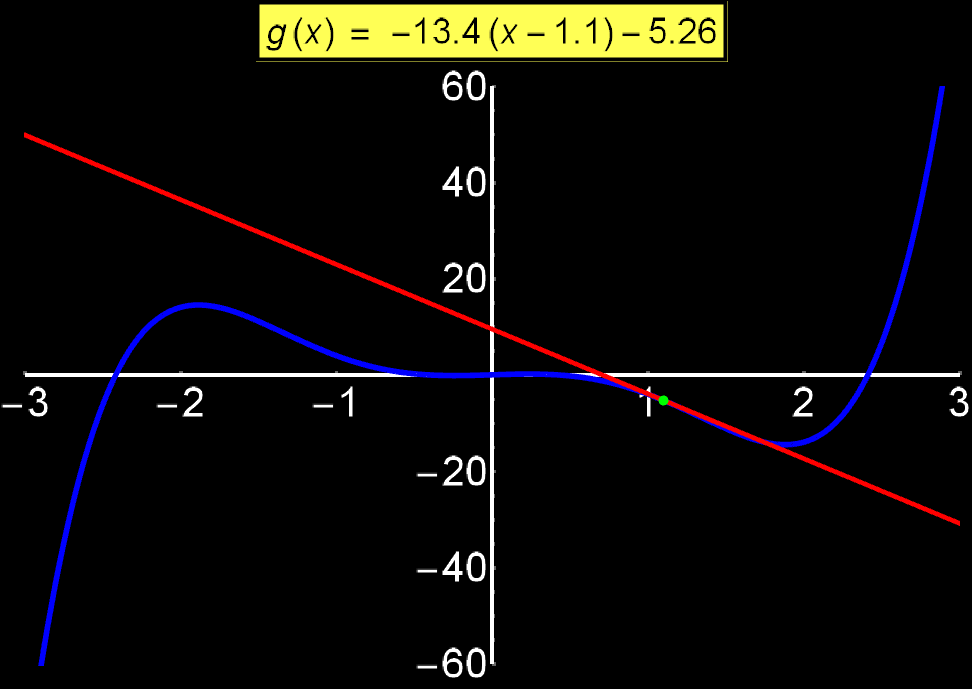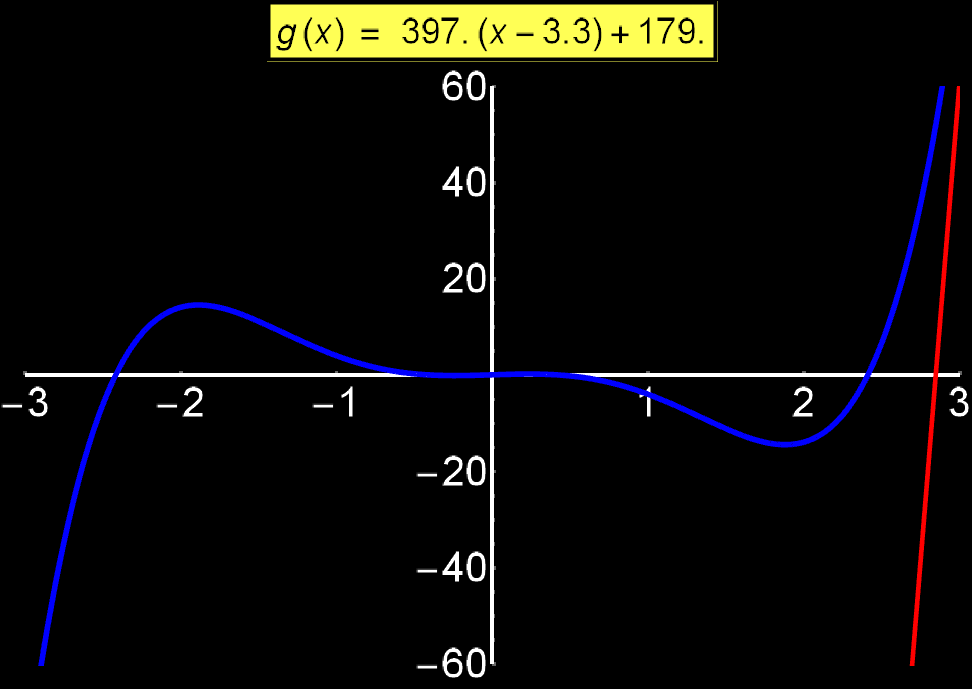
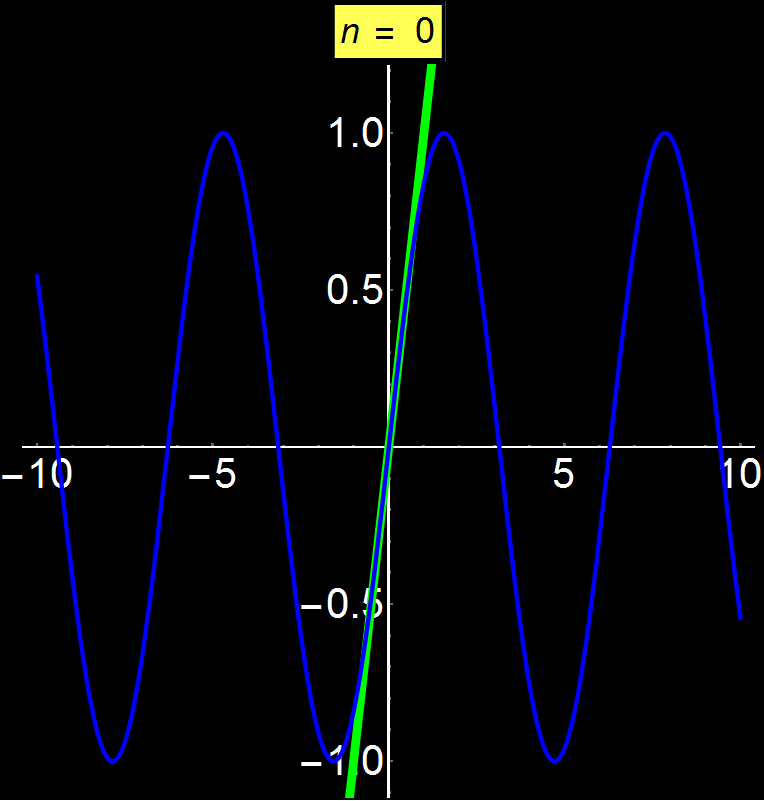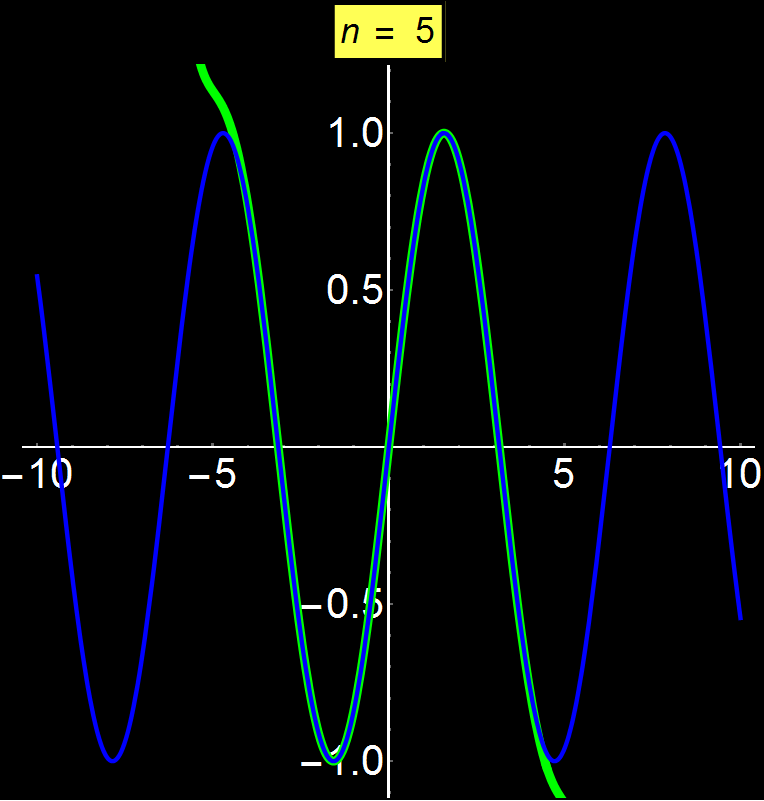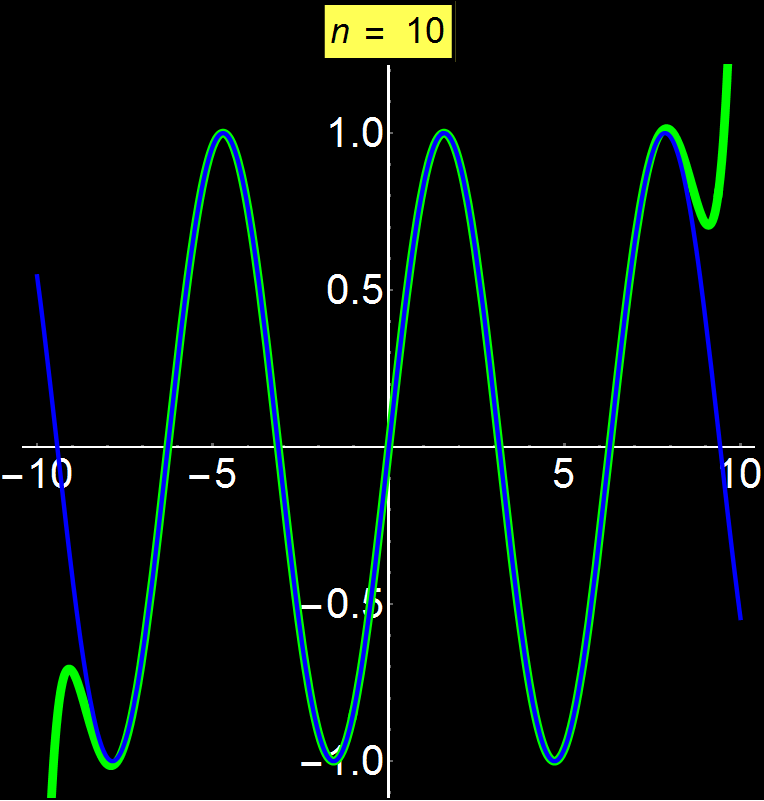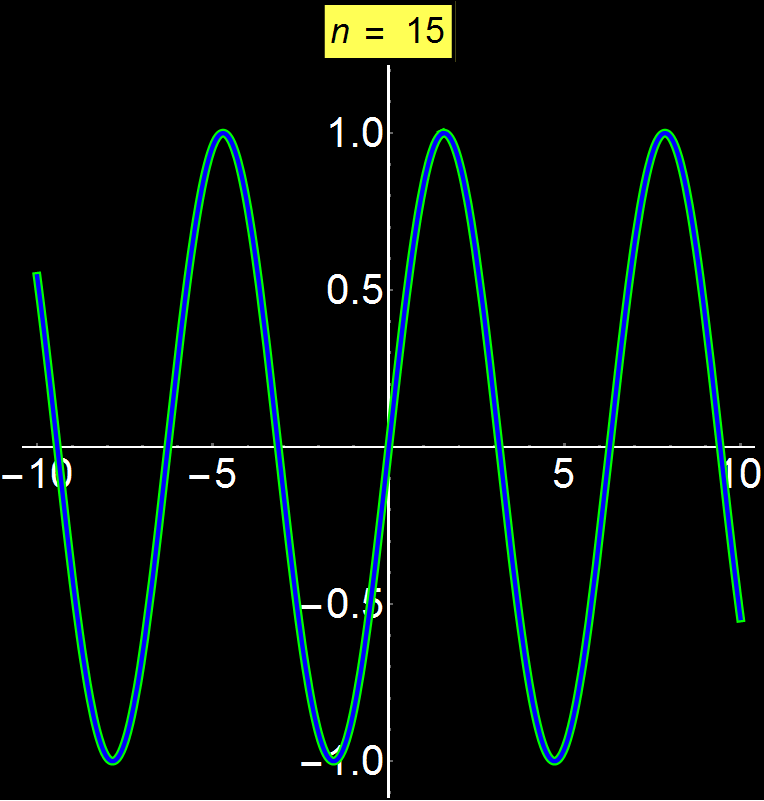
Example 4: Converging Series | Concerns: Graduate Students
Taylor series allow us to represent any function as a sum of infinite terms. Depending on the function, the series can converge anywhere, at a given interval, or even at a single point (center of series). In this example I show the function sin(x) which is a convergent function on all real numbers. We observe that as we increase the number of terms in the series (n), the convergence becomes increasingly better for broader intervals around the center of convergence (here is 0). As n tends to infinity the series converges absolutely with sin(x) throughout the interval of the real numbers.
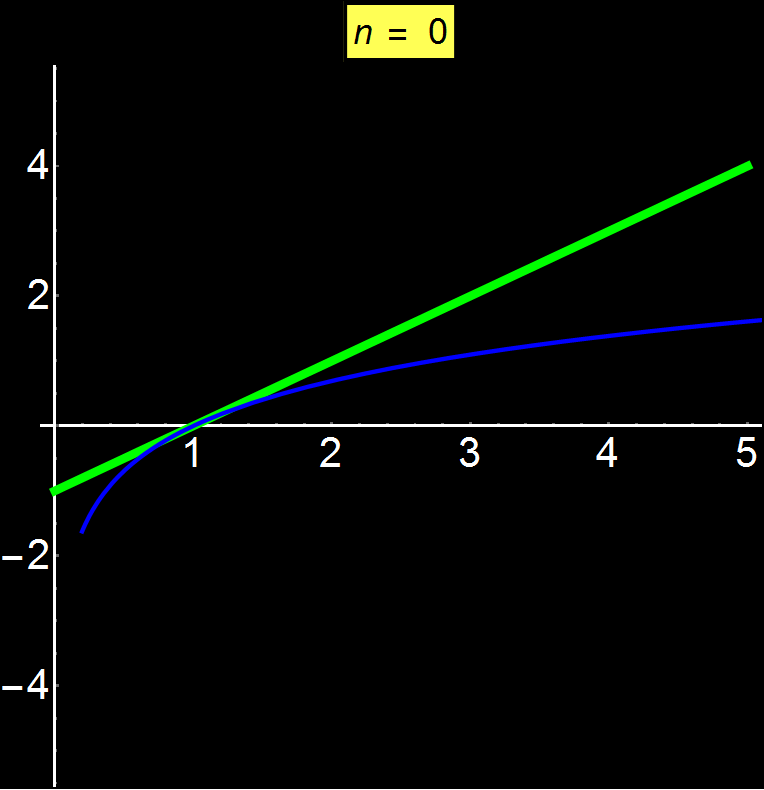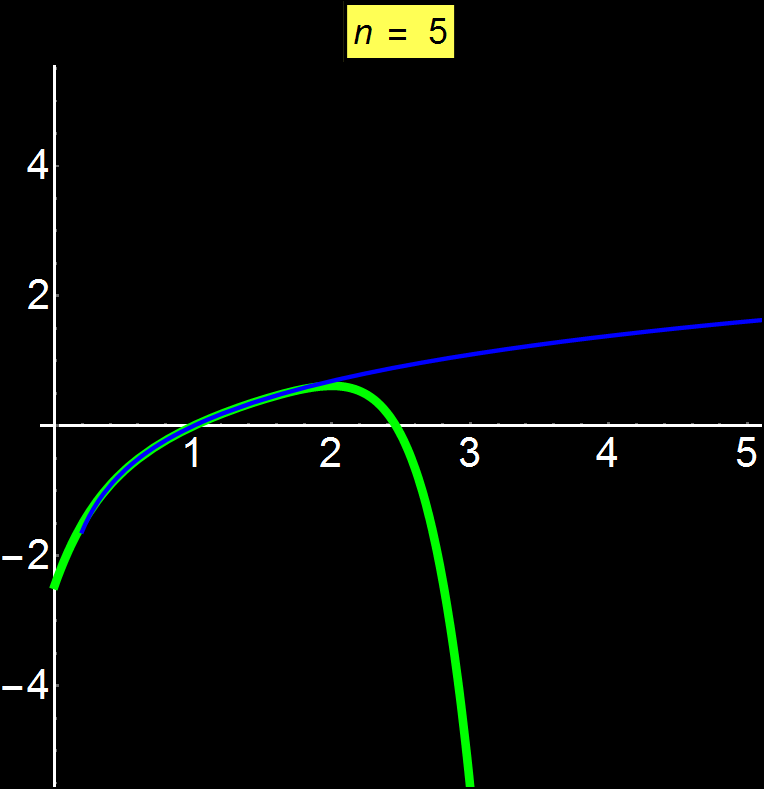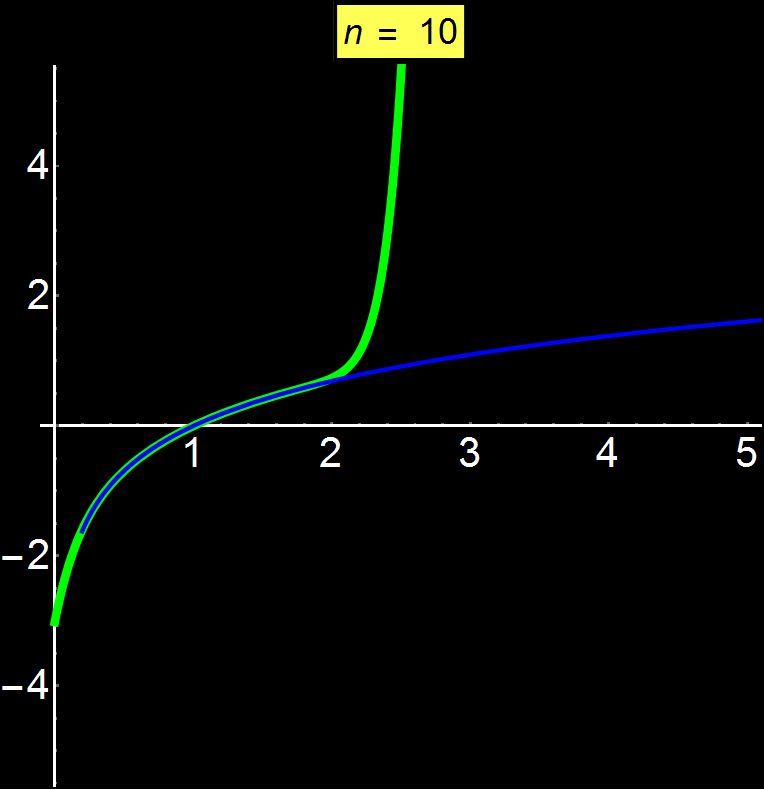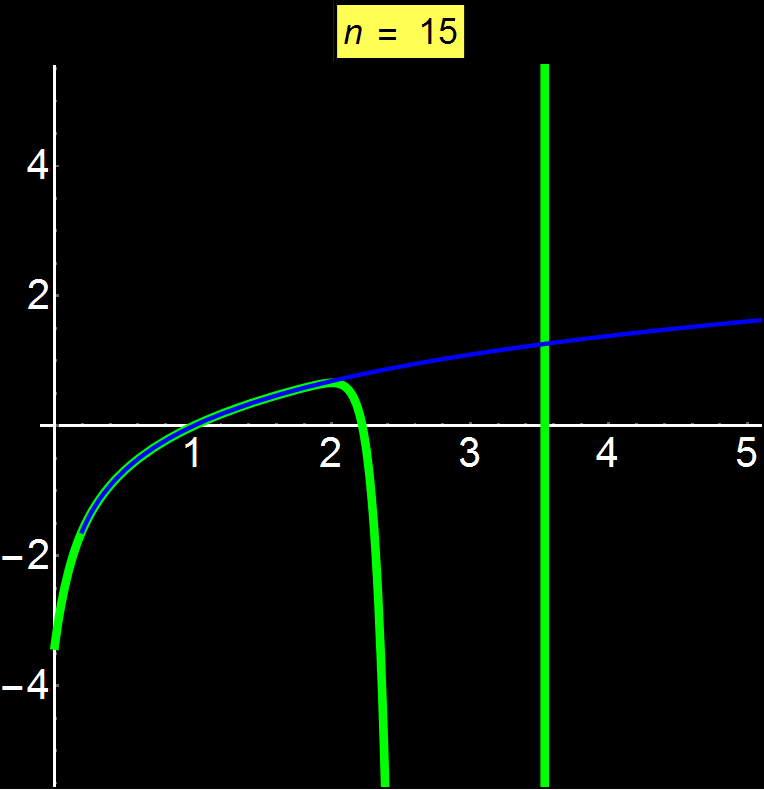
Example 5: Diverging Series | Concerns: Graduate Students
Taylor series allow us to represent any function as a sum of infinite terms. Depending on the function, the series can converge anywhere, at a given interval, or even at a single point (center of series). In this example I show the function ln(x) which is a divergent function above a certain point. We observe that as we increase the number of terms in the sequence (n), it is impossible to converge for x > 2 (here the center of the series is 1). The power series oscillates around 2 without ever being able to converge for x > 2.