Τα μαθηματικά είναι η γλώσσα όλων των θετικών επιστημών, χωρίς αυτά, καμία επιστήμη δεν θα είχε εξελιχθεί στο σημερινό βαθμό. Όπως το αλφάβητο είναι θεμελιώδους σημασίας για να μπορέσει κανείς να μάθει γραφή και ανάγνωση, έτσι και τα μαθηματικά αποτελούν τη βάση όλων των θετικών πεδίων.
Είναι μια αυστηρή επιστήμη με την έννοια οτι η επίλυση προβλημάτων γίνεται με αυστηρούς κανόνες λογικής και αυτός είναι ο λόγος που όσοι επιλύσουν σωστά ένα πρόβλημα πρέπει να βρούν το ίδιο αποτέλεσμα. Αυτός ο ορθολογισμός, μακριά απο υποκειμενισμούς και ερμηνείες, ήταν ένας απο τους λόγους που αγάπησα τα μαθηματικά.
Για να μπορέσει να προχωρήσει ένα άτομο στο χώρο αυτό, απαιτείται η κατανόηση των κανόνων καθώς η αποστήθιση ελάχιστο όφελος έχει. Γι'αυτό τον λόγο είναι κομβικής σημασίας ο καθηγητής να μπορέσει να αναπτύξει τρόπους εκμάθησης που, αφενώς διεγείρουν το ενδιαφέρον, αφετέρου βοηθούν στην κατανόηση την ύλης για τον μαθητή/φοιτητή. Πάνω σε αυτό το σκέλος έχω εργαστεί τα τελευταία 10 περίπου χρόνια έχοντας αναπτύξει μεθόδους που βασίζονται στην πολυαισθητηριακή μάθηση.
Η πολυαισθητηριακή μάθηση αποτελεί έναν απο τους πλέον αποτελεσματικούς τρόπους διδασκαλίας [1, 2, 3]. Πιο συγκεκριμένα δημιουργώ υλικό τέτοιο ώστε ο μαθητής/φοιτητής να αντιλαμβάνεται και να επεξεργάζεται την πληροφορία με όσο το δυνατόν περισσότερες αισθήσεις.
Παρακάτω παραθέτω μερικά παραδείγματα του τρόπου διδασκαλίας μου.
Παράδειγμα 1: Η έννοια του Ορίου | Αφορά: Μαθητές & Φοιτητές
Ορισμός του ορίου μιας συνάρτησης μέσω κινούμενων γραφικών. Όταν η απόσταση (h) 2 διαδοχικών σημείων είναι σχετικά μεγάλη, ο ορισμός του ορίου (κίτρινο πλαίσιο) αποκλίνει απο την πραγματική τιμη f'(1) = 5. Όσο όμως η απόσταση μικραίνει, το όριο τείνει να γίνει ίσο με την πραγματική τιμή. Στην περίπτωση που το h γίνει τόσο μικρό που θεωρείται 0, τότε η κόκκινη ευθεία είναι η εφαπτομένη της συνάρτησης στο x = 1. Αυτός είναι και ο λόγος που το όριο
Σαν συνέπεια των παραπάνω, όταν η κόκκινη ευθεία (εφαπτομένη) γίνει παράλληλη στον x-άξονα τότε η συνάρτηση f(x) δεν μεταβάλλεται γύρω απο αυτό το σημείο οπότε f(x) = f(x0) και το

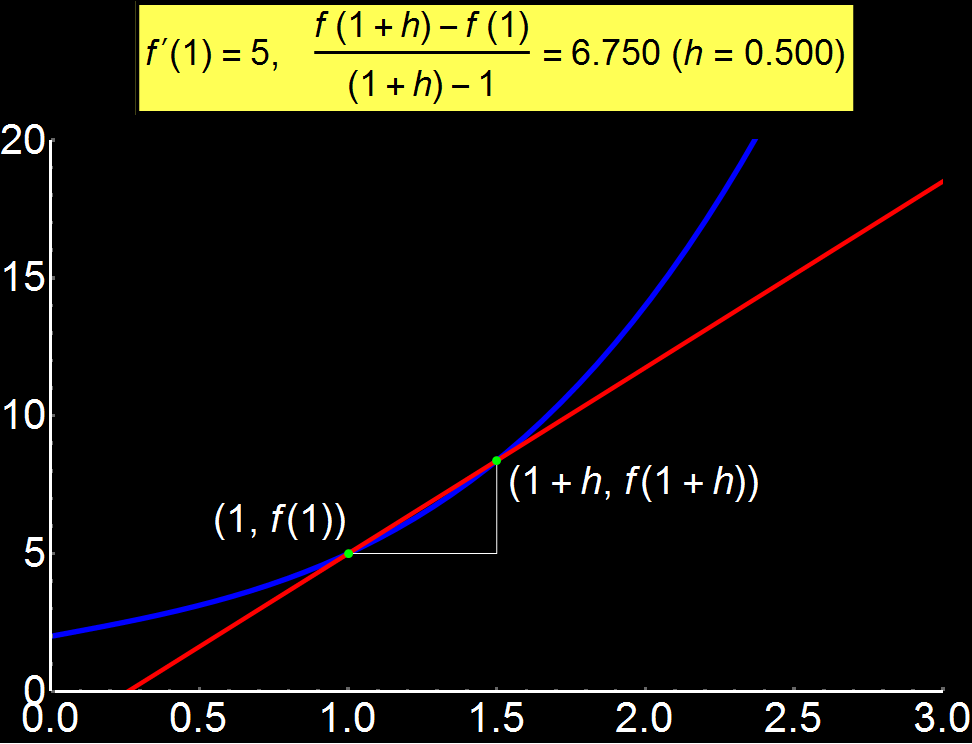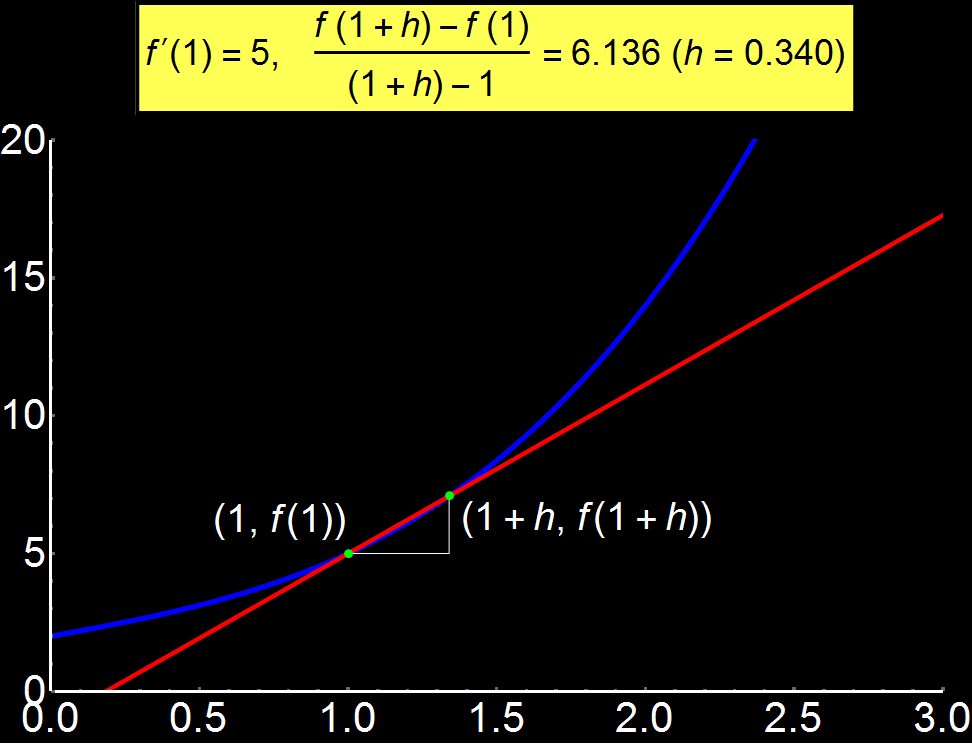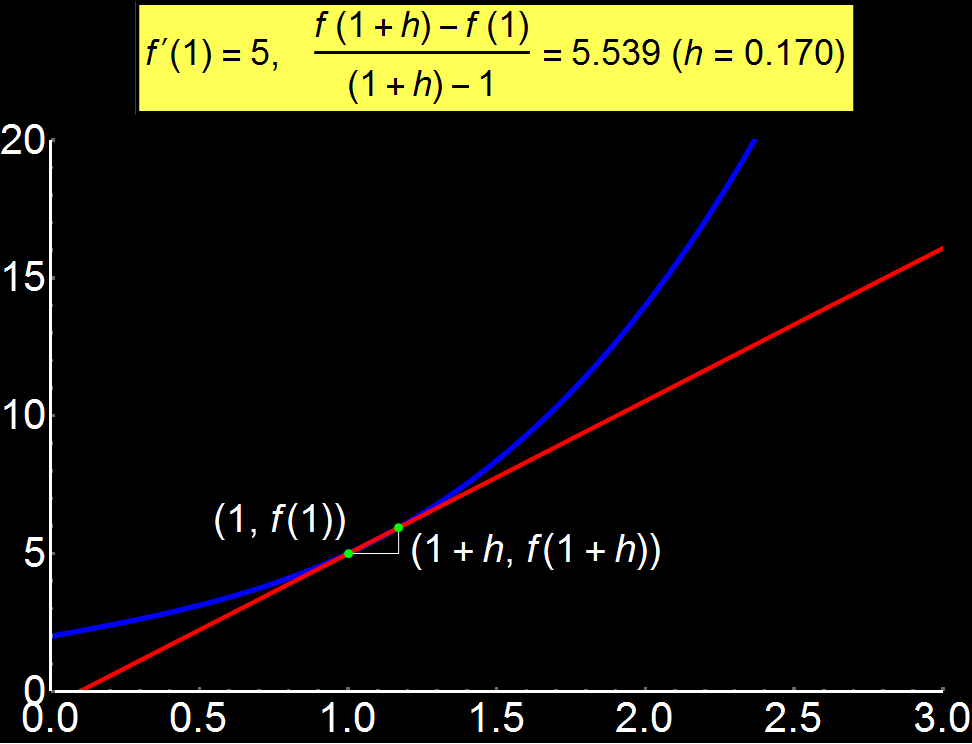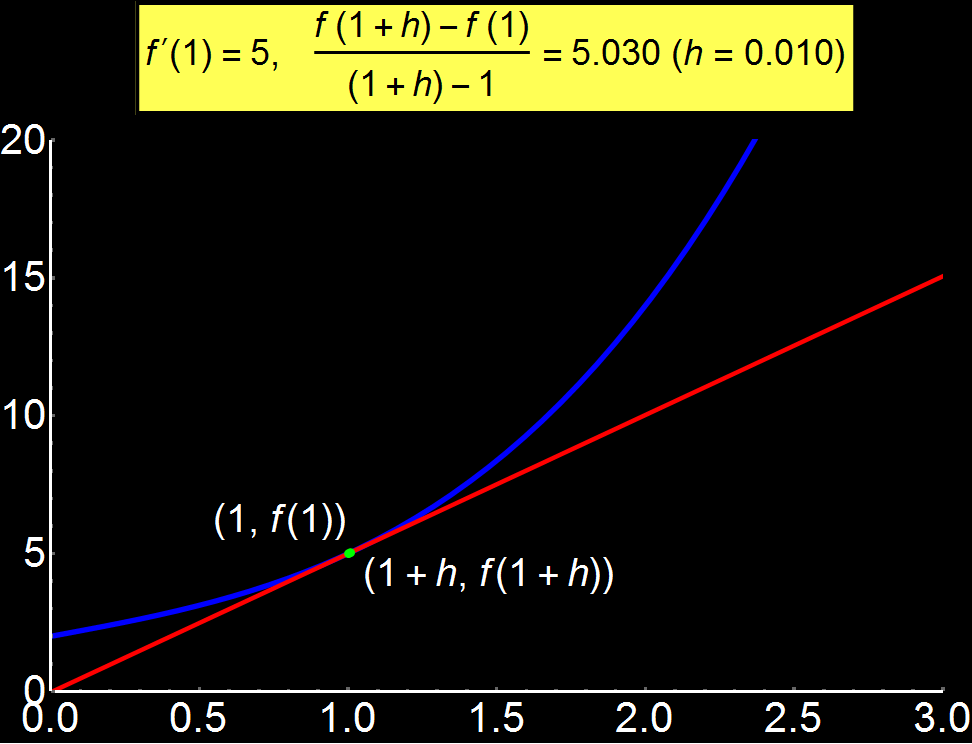
όριο μηδενίζεται. Αντίθετα, στην περίπτωση όπου η κόκκινη ευθεία είναι παράλληλη στον y-άξονα τότε η μεταβλητή x δεν μεταβάλλεται γύρω απο αυτό το σημείο οπότε x = x0 μηδενίζοντας τον παρανομαστή και έτσι το όριο δεν ορίζεται.
Παράδειγμα 2: Η έννοια του Ολοκληρώματος | Αφορά: Μαθητές & Φοιτητές
Ο ορισμός του ολοκληρώματος είναι απο τις πιο δύσκολες έννοιες για έναν μαθητή. Στο διπλανό γράφημα δείχνω πως, αυξάνοντας την διακριτοποίηση (πλήθος των γκρίζων παραλληλογράμμων), μπορούμε σταδιακά να προσεγγίσουμε την ακριβή λύση του ολοκληρώματος μιας συνάρτησης (βλ. κίτρινο πλαίσιο). Συνεπώς, όσα περισσότερα γρίζα παραλληλόγραμμα έχουμε, τόσο καλύτερη η σύγκλιση της προσεγγιστικής τιμής με το αναλυτικό ολοκλήρωμα. Στην οριακή περίπτωση που το πλήθος των παραλληλογράμμων τείνει στο άπειρο έχουμε:

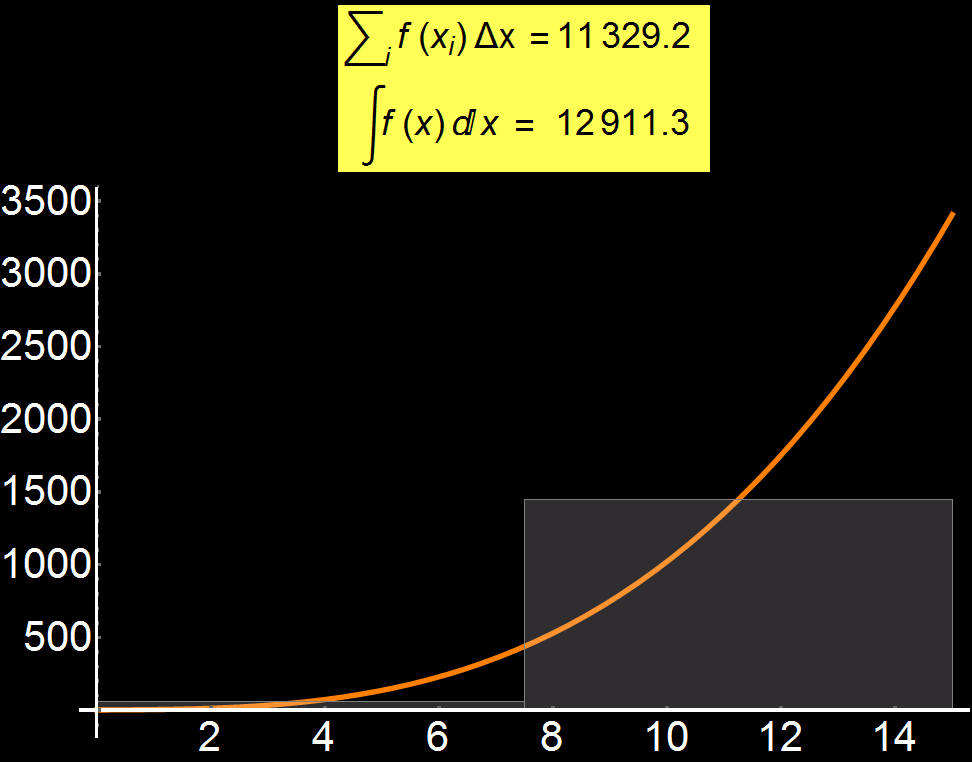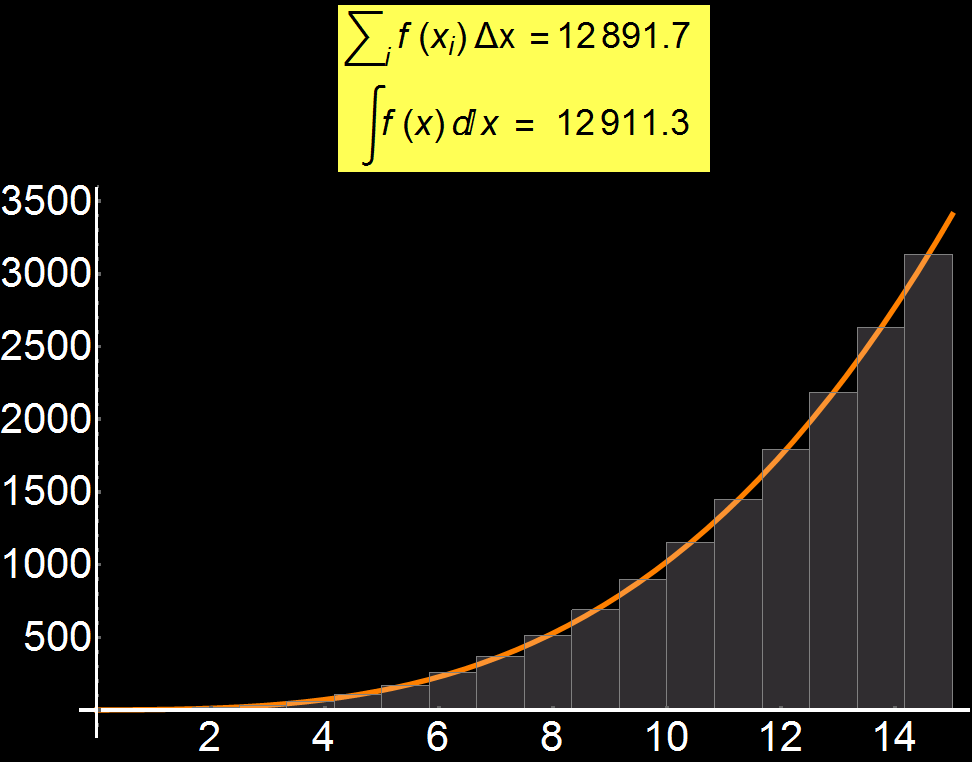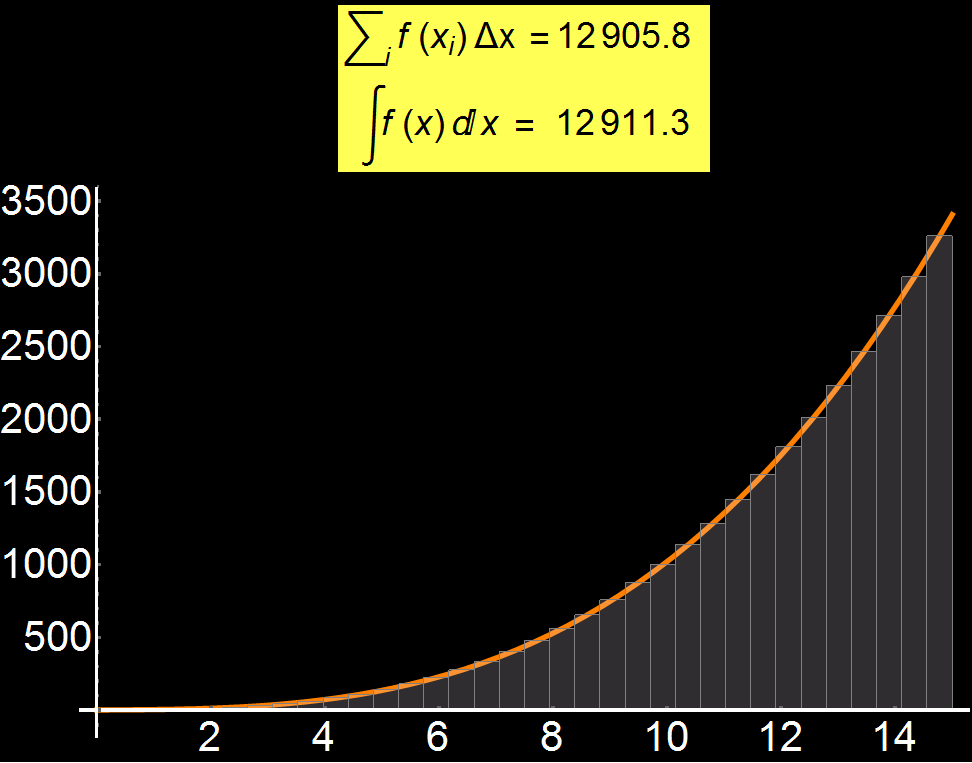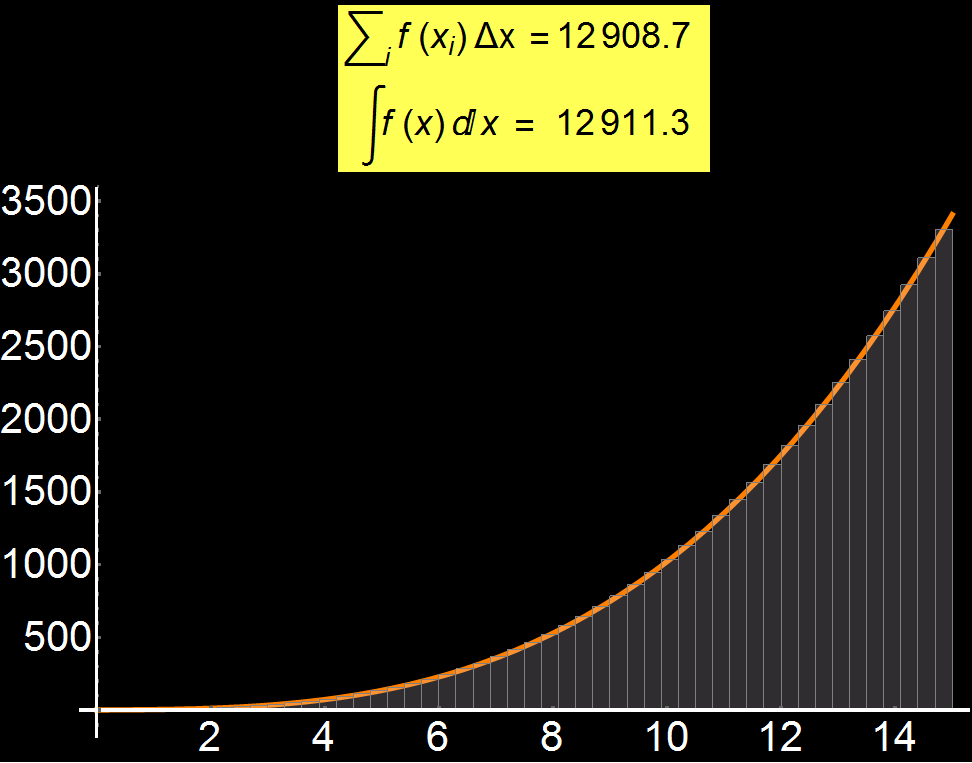
Σε πολλά πρακτικά προβλήματα, το ολοκλήρωμα είναι αδύνατο να υπολογισθεί αναλυτικά και έτσι χρησιμοποιούνται αριθμητικές προσεγγίσεις όπως αυτή που δείχνω εδώ.
Παράδειγμα 3: Εξίσωση Εφαπτομένης | Αφορά: Μαθητές & Φοιτητές
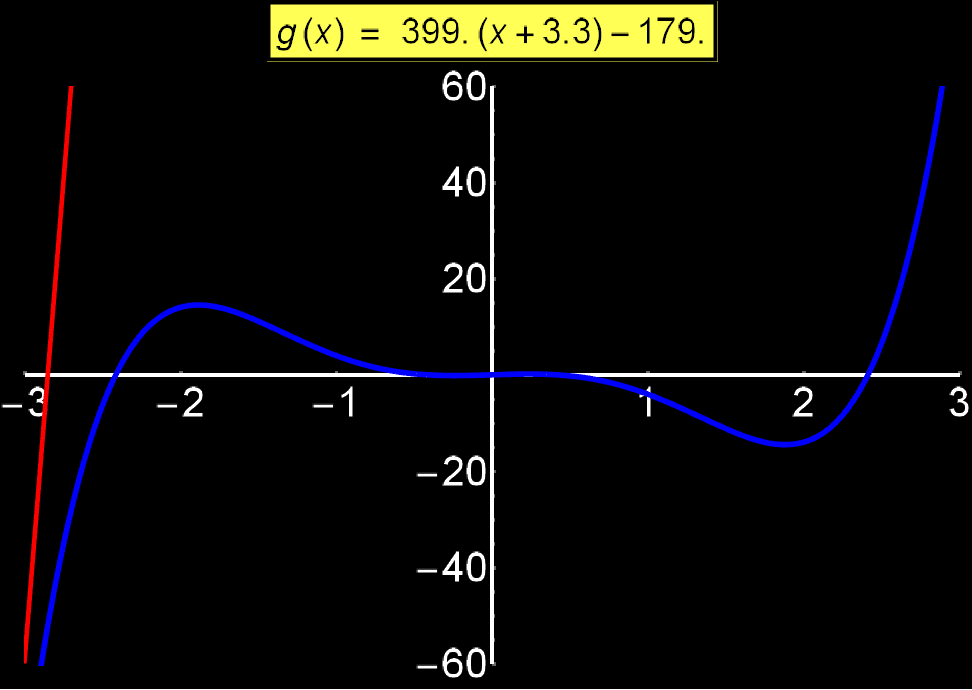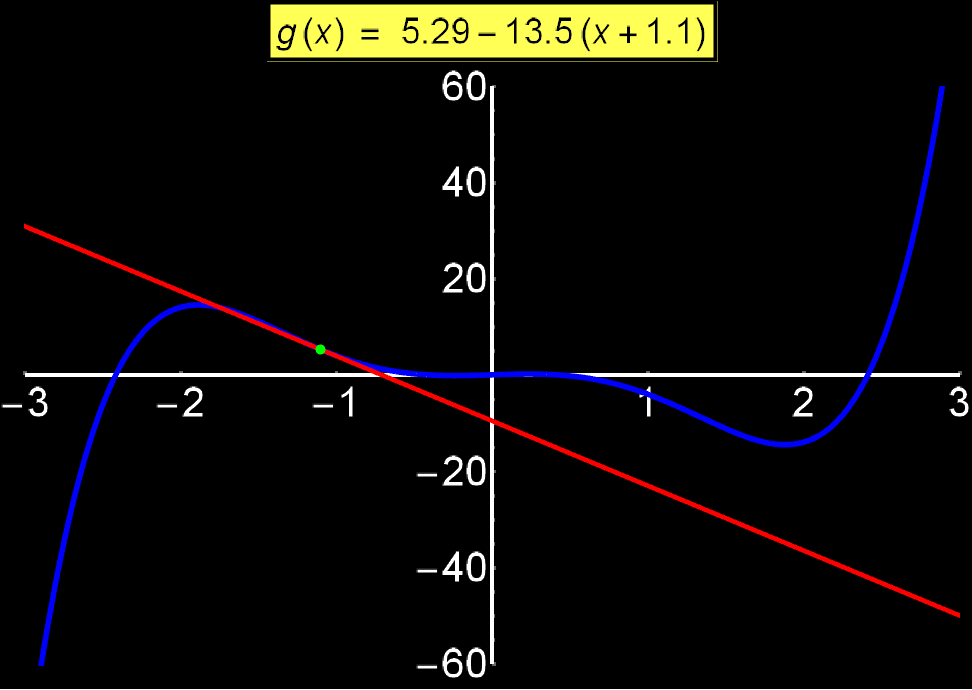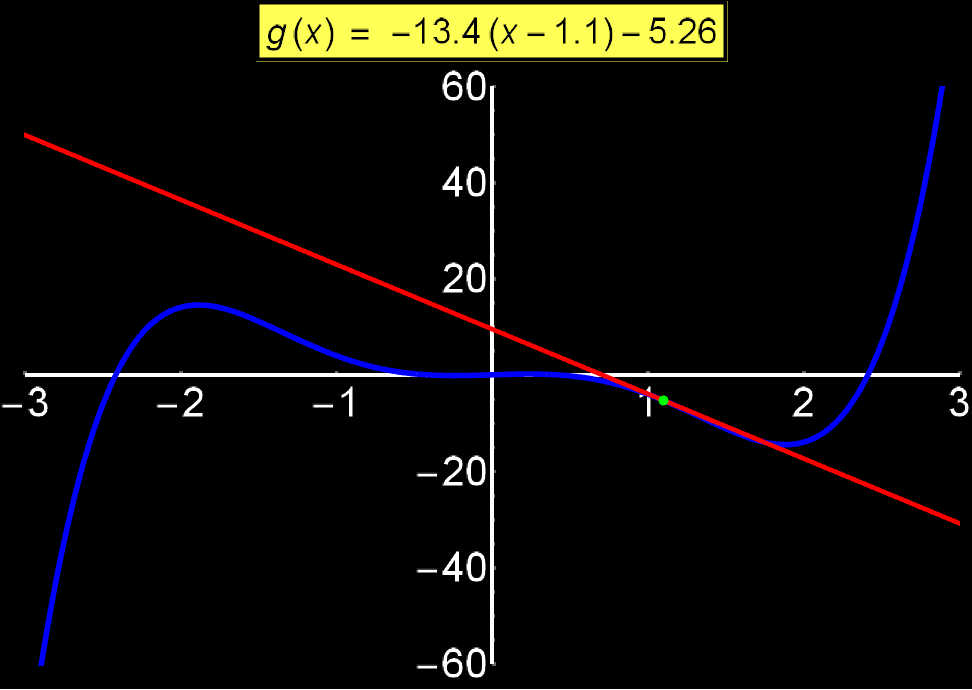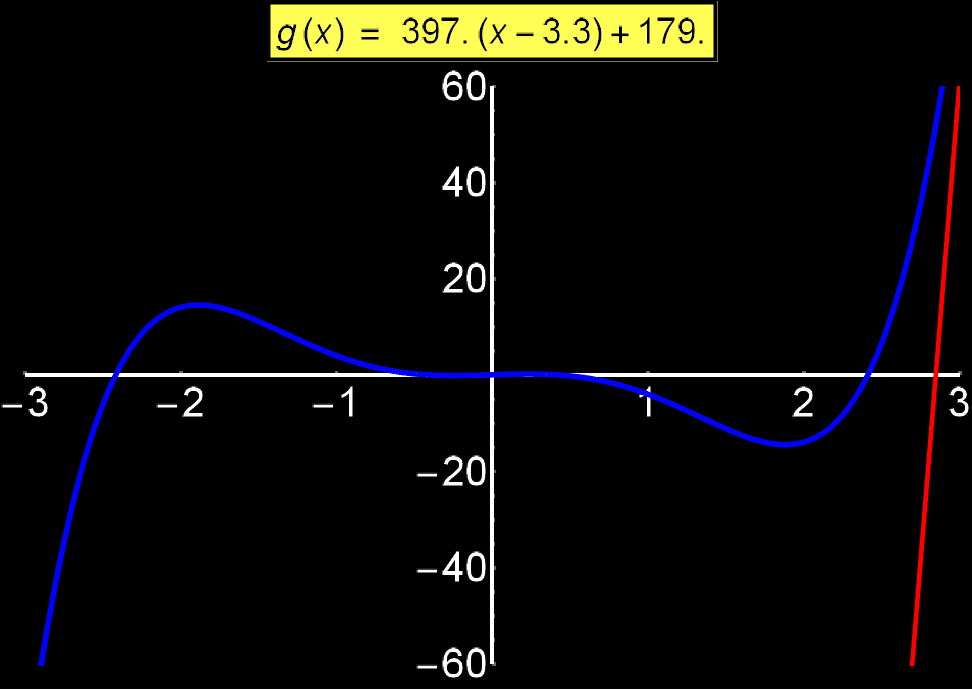
Η εξίσωση εφαπτομένης μιας συνάρτησης f(x) μας δείχνει την κλίση της σε κάθε σημείο {x0, f(x0)}. Μας λέει δηλαδή το πόσο 'απότομη' είναι η συνάρτηση σε κάθε σημείο της. Δίνεται απο την έκφραση:
Στο διπλανό γράφημα δείχνω πώς μεταβάλεται η εφαπτομένη (κόκκινη ευθεία) καθώς 'σαρώνει' μια συνάρτηση f(x) (μπλε καμπύλη). Παρατηρούμε οτι γύρω απο τις τιμές +3 και -3 η μπλέ καμπύλη αλλάζει απότομα, σαν συνέπεια, η αριθμητική τιμή της κλίσης της εξ. εφαπτομένης παίρνει μεγάλες τιμές (f'(x0) ~ 400). Αντίθετα, γύρω απο το 0 όπου η μπλέ καμπύλη αλλάζει ελαφρώς, η κλίση παίρνει μικρές τιμές (f'(x0) ~ 1).
Παράδειγμα 4: Συγκλίνουσες Σειρές | Αφορά: Φοιτητές
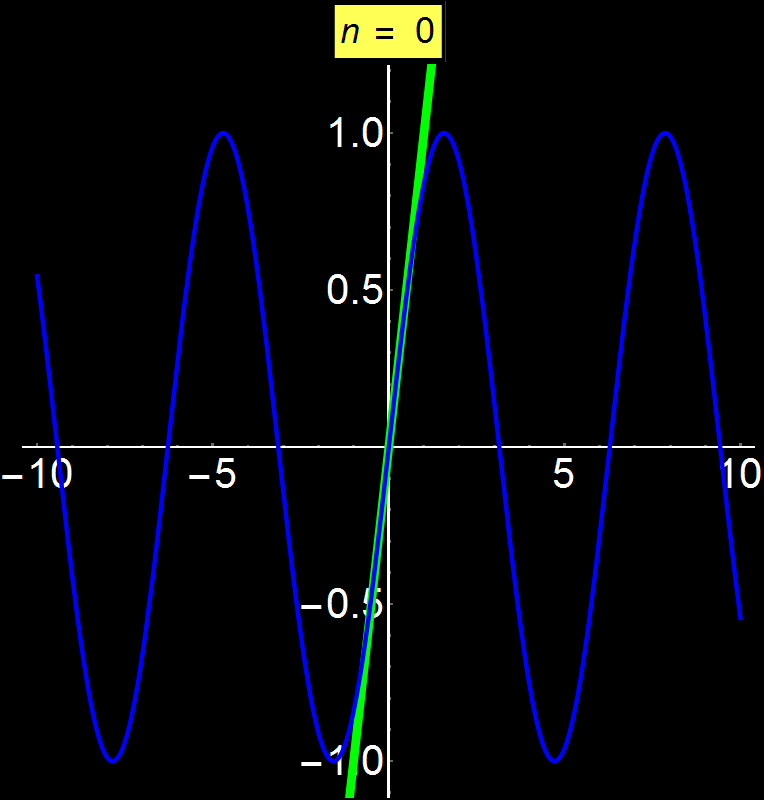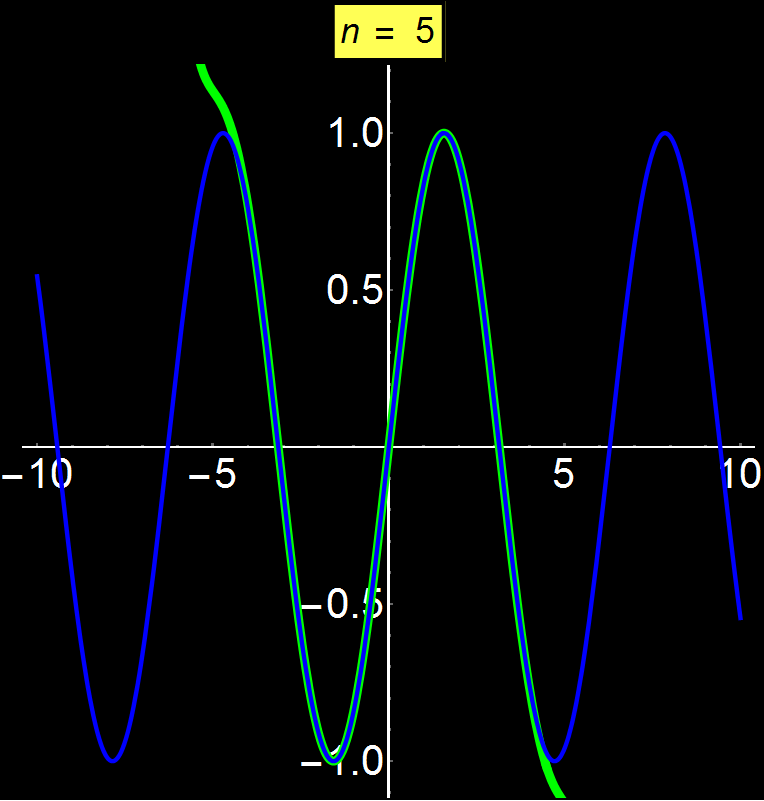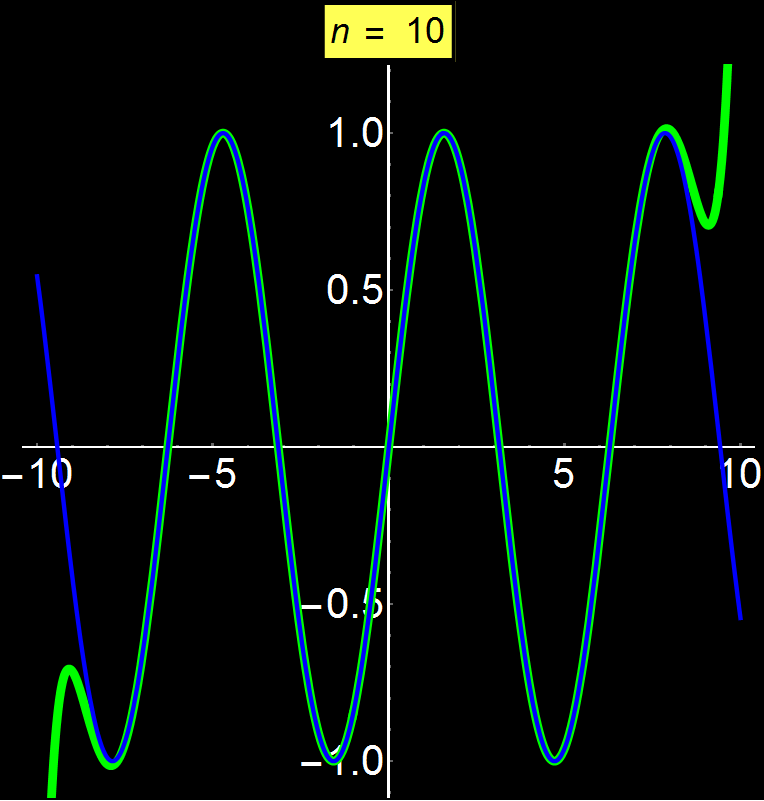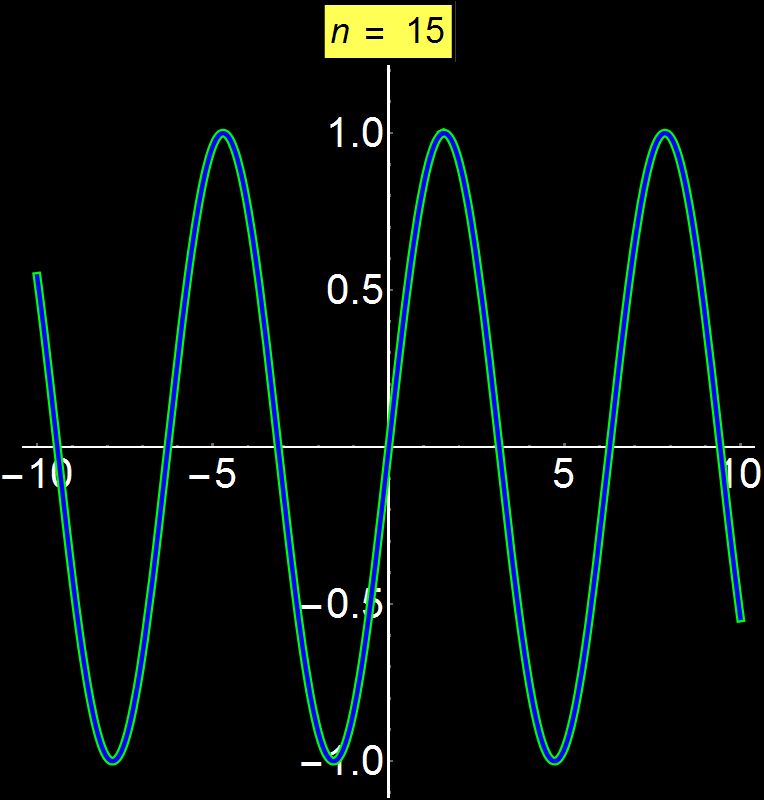
Οι δυναμοσειρές Taylor μας επιτρέπουν να αναπαραστήσουμε οποιαδήποτε συνάρτηση ως άθροισμα άπειρων όρων. Ανάλογα με τη συνάρτηση, η σειρά μπορεί να συγκλίνει παντού, σε ένα συγκεκριμένο διάστημα ή ακόμα και σε ένα μόνο σημείο (κέντρο σειράς). Στο παράδειγμα αυτό δείχνω τη συνάρτηση ημ(x) η οποία είναι μία συγκλίνουσα συνάρτηση σε όλους τους πραγματικούς αριθμούς. Παρατηρούμε ότι καθώς αυξάνουμε το πλήθος των όρων της σειράς (n), η σύγκλιση γίνεται όλο και καλύτερη για ολοένα μεγαλύτερα διαστήματα γύρω από το κέντρο σύγκλισης (εδώ το 0). Καθώς το n τείνει στο άπειρο η σειρά συγκλίνει απόλυτα με το ημ(x) σε όλο το διάστημα των πραγματικών αριθμών.
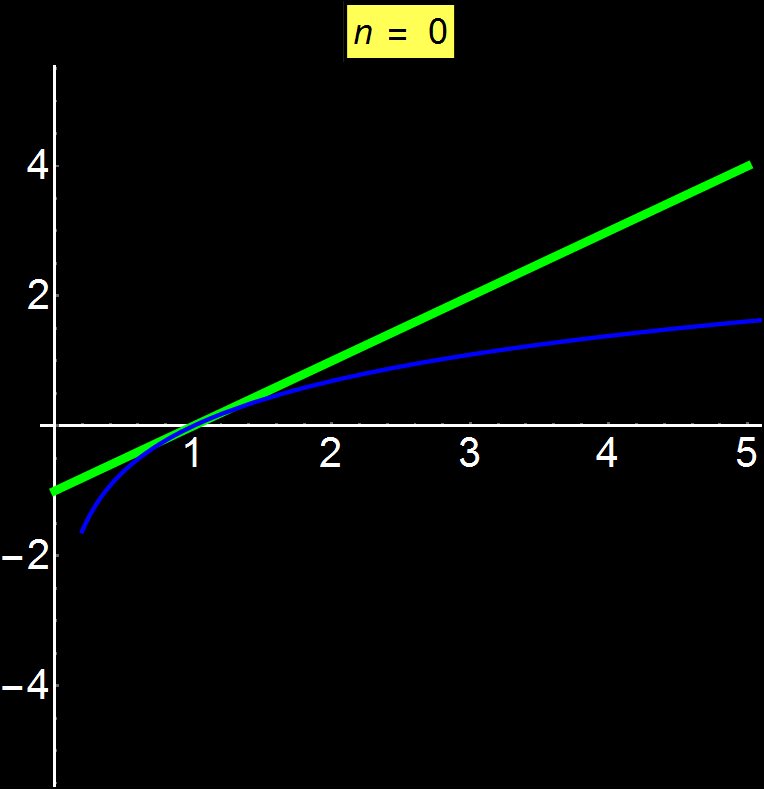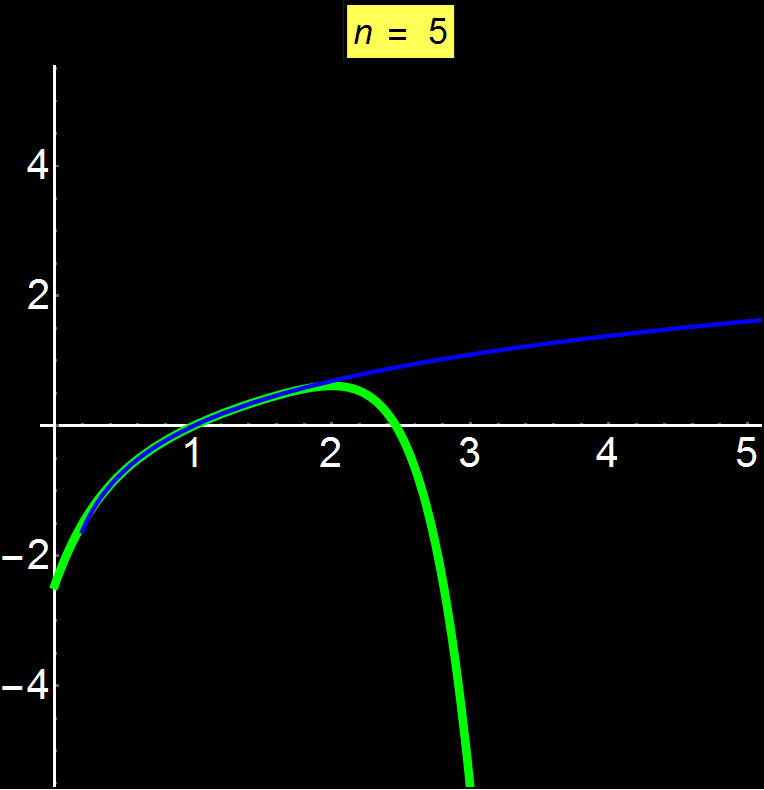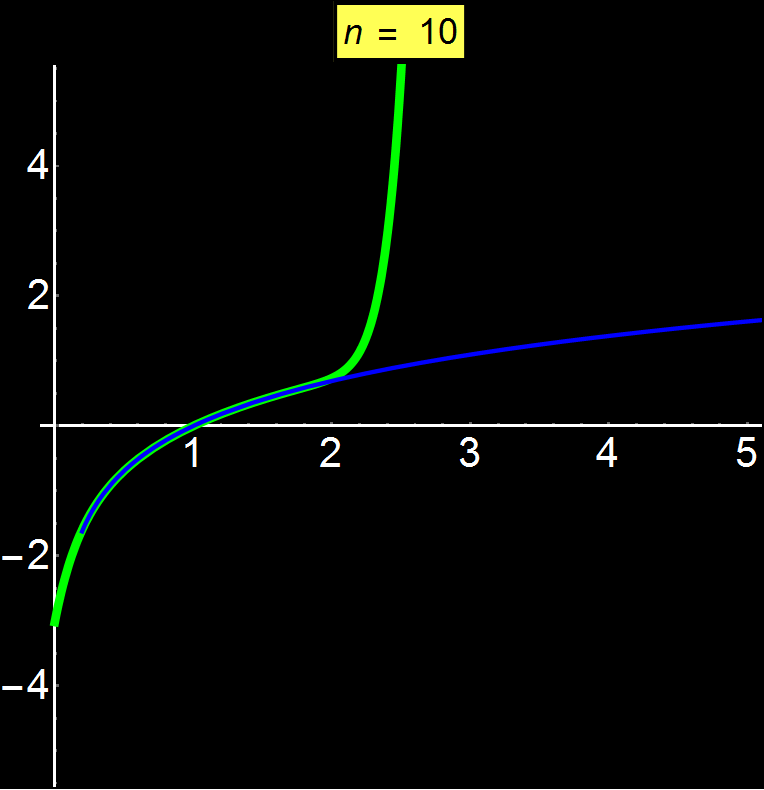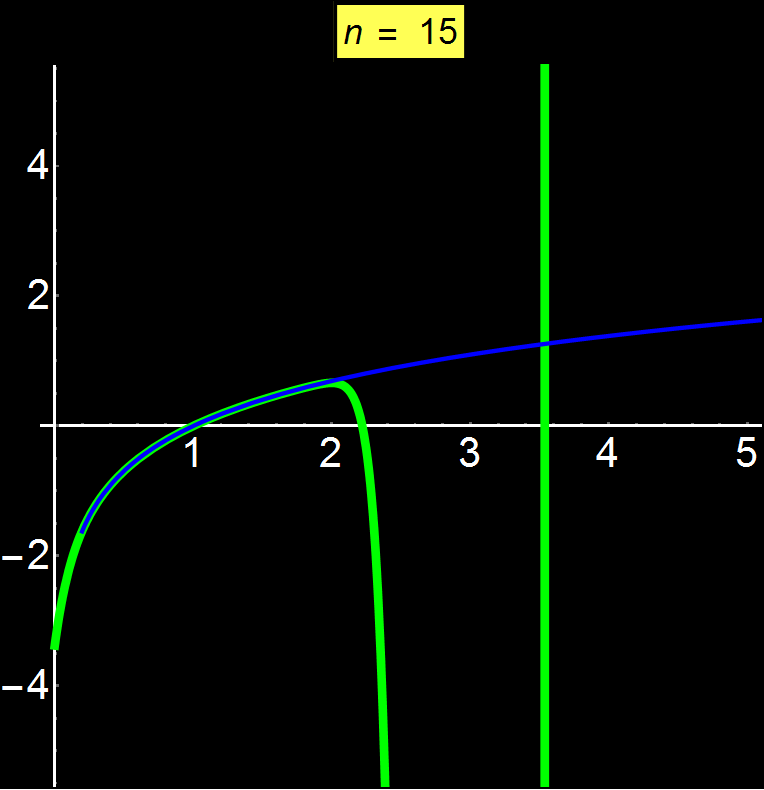
Παράδειγμα 5: Αποκλίνουσες Σειρές | Αφορά: Φοιτητές
Οι δυναμοσειρές Taylor μας επιτρέπουν να αναπαραστήσουμε οποιαδήποτε συνάρτηση ως άθροισμα άπειρων όρων. Ανάλογα με τη συνάρτηση, η σειρά μπορεί να συγκλίνει παντού, σε ένα συγκεκριμένο διάστημα ή ακόμα και σε ένα μόνο σημείο (κέντρο σειράς). Στο παράδειγμα αυτό δείχνω τη συνάρτηση ln(x) η οποία είναι μία αποκλίνουσα συνάρτηση από κάποιο σημείο και μετά. Παρατηρούμε ότι καθώς αυξάνουμε το πλήθος των όρων της σειράς (n), είναι αδύνατη η σύγκλιση για x > 2 (εδώ το κέντρο της σειράς είναι το 1). Η δυναμοσειρά ταλαντώνεται γύρω από το 2 χωρίς ποτέ να μπορεί να συγκλίνει για μεγαλύτερες του 2 τιμές.